알고보면 유용한 삼각함수 곱셈 공식

고등학교 수학II 과목에서 배우는 개념이 삼각함수이다. 사실 삼각함수 단원에서, 왜 배워야 하는지, 어디에 쓰이는지 잘 배우지 못하고, 설명도 없이 공식을 외우고 문제를 풀었다.

삼각함수의 가치는 우리 자연계의 현상 대부분이 주기성을 갖고 있다는 사실에 있다. 그 주기성을 갖는 자연현상을 설명하는 데 삼각함수가 아주 유용하게 쓰인다. 태양을 중심으로 공전하는 지구, 지구의 자전을 비롯한 우주의 현상뿐만 아니라 우리 몸 속의 심장의 박동도 주기성을 갖고 있다.

4차 산업혁명으로 들어오면 반도체 내의 회로, 컴퓨터도 주기를 갖는 시계(clock)에 맞추어 서로 약속된 동작을 한다. 5G 통신에서도 3.4~6GHz, 혹은 28GHz 전자파를 사용하게 되는데, 이 전자파도 주기성을 갖는 삼각함수 (sine wave)이면서 공간으로 빛의 속도로 전파한다. 이때 1초에 시간에 따라 신호가 진동하는 횟수를 주파수(f, frequency)라고 한다.

수학II 과목에서 삼각함수의 특징을 이해하고 해석하기 위해서 여러 종류의 수식을 배우고 실습한다. 그런데 수식이 복잡해서 단순히 외워서 사용했다. 그 중에서 가장 복잡한 수식이 삼각함수 곱하기 공식이다. 두 개의 삼각함수가 곱해지면 그 결과가 어떻게 되는가 하는 결과를 보여 주는 수식이다.

공식에 의하면 예를 들어 주파수 f1 인 삼각함수와 주파수 f2 인 삼각함수가 곱해지면 새로운 삼각함수가 만들어 진다. 그런데 그 새 삼각함수의 주파수가 f1+f2, f1-f2 로 생성된다. 이처럼 새로운 삼각함수의 주파수는 기존의 두 개의 주파수 합과 주파수 차로 이루어진 새로운 2 개의 서로 다른 주파수를 가진 삼각함수가 만들어 진다.

따라서 자연계에서 두 개의 각각 다른 주기를 가진 현상이 만나서 곱하기 동작을 하면 새로운 주파수가 만들어지는 현상을 이처럼 설명할 수 있다. 일종의 주파수 더하기, 빼기 혹은 변환기가 되는 셈이다. 5G 통신을 위한 송수신 회로에는 이러한 주파수 곱하기 기능을 담당하는 소자를 신호 혼합기(Mixer)라고 부른다. 주로 반도체 트랜지스터의 비선형성 성질을 이용해서 수학적으로는 곱하기, 기능적으로는 신호 혼합기가 이런 역할을 만든다. 반도체 트랜지스터의 불량한 비선형 성격을 이용해서 곱하기를 한다.

그러니 고등학교 때 배운 삼각함수 곱하기 공식의 원리는 5G 통신 시스템에 핵심적으로 사용하는 원리로 사용된다. 그걸 고등학교 때 미리 알기는 어렵겠다.

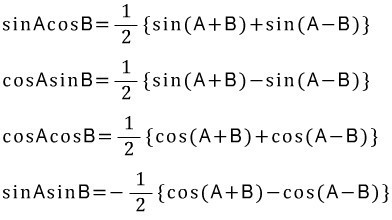
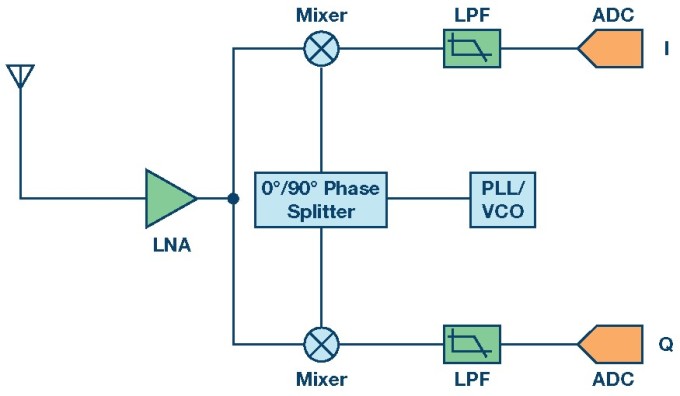
5G 송수신기에 필요한 신호 혼합기

5G 통신에서 고주파 전자파를 사용하려는 이유는 제일 먼저 무선통신으로 보내는 데이터 용량을 높이기 위해서이다. 그런데 고주파를 사용하면 신호 감쇄가 크고, 전파의 직진성이 크다. 그대신 전자파 파장의 크기가 작아 안테나 크기를 줄일 수 있다. 한편 5G 무선 통신 시스템에는 이와 같은 안테나뿐만 아니라, 증폭기(LNA, Low Noise Amplifier), 신호 혼합기(Mixer), 저대역 필터(잡음 제거기), ADC(아날로그 디지털 변환기) 등이 포함된다. 이 소자들 역시 고주파 대역의 특징을 잘 살려 설계해야 한다.

그런데 여기에서 고주파 전자파에 디지털 데이터 신호를 싣는 장치가 바로 신호 혼합기(Mixer)이다. 여기에서 전자파와 디지털 데이터가 수학적으로 곱해진다. 그러면 이 혼합기에서 전자파 주파수 fr 과 디지털 데이터 주파수 fd 가 섞이게 된다. 그래서 새로운 주파수 fr+fd, fr-fd 가 새로 생성된다. 디지털 데이터 신호를 그대로 공간으로 전파할 수 없다. 공간으로의 전파는 고주파 전자파를 이용해야 한다.

그래서 이 신호 혼합기에서 두 신호를 섞어야 한다. 이처럼 고등학교 수학 교과서에 배운 삼각함수 곱셈 공식의 원리가 5G 통시 시스템에서 고주파 전자파 주파수와 디지털 데이터 전자파 주파수를 섞는 원리가 된다.

RF 신호 혼합기(Mixer)가 포함된 모듈 사진. [출처: 디지키(Digikey)]

다양한 분야의 융합 통해 혁신해야 

5G 통신 시스템에서는 신호 혼합기에서 보는 사례처럼, 실제 서로 다른 신호, 서로 다른 주파수, 서로 다른 영역의 기술이 융합되는 경우가 많이 있다. 그 융합은 디지털 신호와 아날로그 신호, 디지털 신호와 고주파 신호, 전력 전송과 신호 전달 등 서로 다른 분야가 합쳐져서 구현되고 있다. 4차 산업혁명 시대의 새로운 기술은 다양한 영역의 기술 융합으로부터 나올 수 밖에 없다.

새로운 산업과 일자리 창출도 마찬가지이다. 한 분야만의 혁신은 거의 종말에 가까이 왔다. 이제는 융합을 통한 성장의 시대이다.

4차 산업혁명 시대에는 이러한 융합의 중심이 인공지능과 빅데이터가 될 것으로 예측한다. 특히 인공지능과 빅데이터 기술이 의료, 금융, 보험, 행정, 교육, 서비스, 교통, 환경, 생산, 에너지, 자원, 우주 등 다양한 전 분야와 결합해서 효율을 높이고 생산성을 향상 시킬 것으로 본다. 긍정적으로 본다면 인간에게 노동, 자원, 시간의 자유를 선물할 수도 있다. 이것이 혁신 성장을 의미한다. 그 혁신성장을 인공지능과 빅데이터 중심의 융합으로 만들 수 있다.

joungho@kaist.ac.kr  

[김정호 카이스트 전기 및 전자공학과 교수]